Purely functional data structures in Clojure: Red-Black Trees
This post is part of a series about Chris Okasaki’s Purely Functional Data Structures. You can see all posts in the series by visiting the functional-data-structures category in this blog.
Recently I had some free time to come back to Purely Functional Data Structures and implement a new data structure: Red-black trees.
Red-black trees
Red-black trees are a type of self-balancing binary search tree. Back when I first learned the balancing algorithm used in operations such as insert and delete, I remember it being a particularly tricky one.
Traditionally, red-black trees are implemented destructively - meaning insertions and deletions happen in place. So in imperative languages like C or Java there is a lot of node pointer manipulation floating around, making this algorithm error prone.
This post, as its title implies, will deal with the functional implementation which, besides simpler, is also persistent.
Invariants
A big disadvantage of binary search trees is that they operate poorly on sorted data with O(N) worst case, pretty much becoming nothing more than a linked list.
This is where Red-black trees come in: when inserting/removing new nodes, the tree balances itself thus guaranteeing search times of O(logN). It does so by satisfying two invariants:
- No red nodes can have red children
- Every path from the root to an empty node contains the same number of black nodes
The image below - taken from the book itself - concisely summarises the 4 cases involved in these invariants, starting at the top and then moving counter-clockwise.
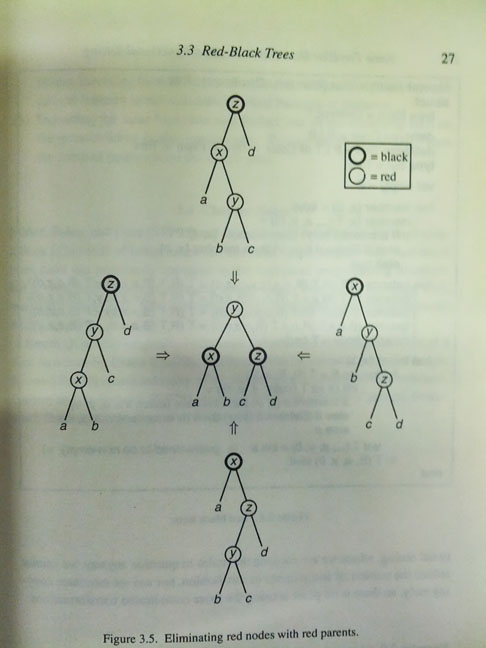
With this in mind I set out to write the balance function in Clojure.
The code
In the functional version of a Red-black tree all pointer manipulation required in its destructive counterpart simply disappears, rendering the algorithm a lot simpler.
Nevertheless, we’re left with some complexity in the balance function around testing a node’s colour as well as its children’s and grandchildren’s.
My first attempt at writing it started like this:
(defn mk-tree [color left value right]
{:color color :left left :value value :right right})
(defn balance [tree]
;; case 1
(let [{z :value d :right} tree
{x-color :color x :value a :left} (-> tree :left)
{y-color :color y :value b :left c :right} (-> tree :left :right)
d (:right tree)]
(if (and (= x-color :red) (= y-color :red))
(mk-tree :red
(mk-tree :black a x b)
y
(mk-tree :black c z d))
tree)
...))
I was extremely unhappy with this. A lot of boilerplate around bindings and tests. And this is only the first case.
But if you read Okasaki’s implementation of the algorithm in ML - or Haskell - you’ll quickly realise how concise and elegant it is. The main reason for that is pattern matching, something we don’t have built-in in Clojure.
However, Clojure is a Lisp and has a powerful macros system at its disposal. That has given us core.match, a pattern matching library for Clojure.
core.match
Using core.match, I rewrote my balance function:
(defn balance [tree]
(match [tree]
[(:or {:left {:color :red
:left {:color :red :left a :value x :right b}
:value y :right c}
:value z :right d}
{:left {:color :red
:left a :value x
:right {:color :red :value y :left b :right c}}
:value z :right d}
{:left a :value x
:right {:color :red
:left {:color :red
:left b :value y :right c}
:value z :right d}}
{:left a :value x
:right {:color :red
:left b :value y
:right {:color :red
:left c :value z :right d}}})]
(mk-tree :red
(mk-tree :black a x b)
y
(mk-tree :black c z d))
:else tree))
If you look closely at the patterns being matched, you’ll see they cater for all 4 cases and allow for both matching and binding in the same expressions. With only a little over double the size of a single case using the previous function, we now have a fully functioning balance implementation. This is better, but I wanted more.
What I really wanted to be able to write is this:
(defn balance [tree]
(match [tree]
[(:or (Black. (Red. (Red. a x b) y c) z d)
(Black. (Red. a x (Red. b y c)) z d)
(Black. a x (Red. (Red. b y c) z d))
(Black. a x (Red. b y (Red. c z d))))] (Red. (Black. a x b)
y
(Black. c z d))
:else tree))
Unfortunately core.match doesn’t support records/protocols yet. However, while reading core.match’s source code, I found a test that implemented the balance algorithm using a different way of representing a tree.
You see, I went with the map approach because I like how you can ask for the specific keys that represent the parts of the tree, such as :color, :left, :value and :right. But if you’re happy with using positional elements in a vector to represent your tree, our balance function in Clojure becomes this:
(defn balance [tree]
(match [tree]
[(:or [:black [:red [:red a x b] y c] z d]
[:black [:red a x [:red b y c]] z d]
[:black a x [:red [:red b y c] z d]]
[:black a x [:red b y [:red c z d]]])] [:red [:black a x b]
y
[:black c z d]]
:else tree))
Which is amazingly similar to the protocols/records version above.
I guess one of the lessons here is that by carefully choosing the data structure to represent your problem, your implementation can become substantially simpler.
As usual, all code is on github, with the Red-black tree specific section in this direct link. The project also includes tests.
Until next time.